Sampling theorem | Verification of NYQUIST’S sampling theorem using MATLAB

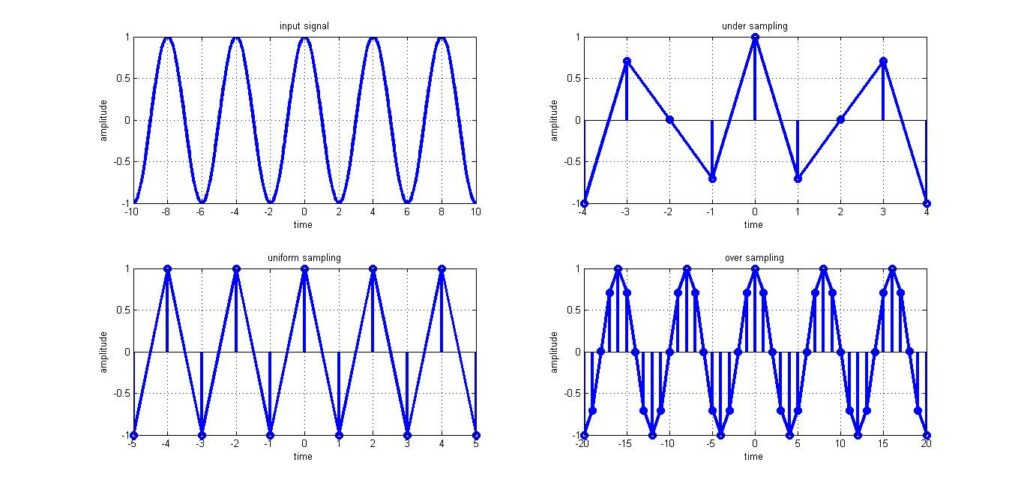
Next we plot the un-sampled signal.

% In time Domain
subplot(421);
xData = sin(2*pi*messageSignalFrequency*timeAxis + phi);
plot(1000*timeAxis, xData, "lineWidth", widthOfTheLine);
set(get(gca, 'XLabel'), 'String', 'Time in milliSeconds  (ms)');
set(get(gca, 'YLabel'), 'String', 'Amplitude');
set(get(gca, 'Title'), 'String', 'Un-Sampled Signal');
grid on;
axis([0 1000*numberOfWaves/messageSignalFrequency -1 1]);
 
% In Frequency Domain
subplot(422);
xDataFFT = fftshift(fft(xData));
semilogx(frequencyAxis, abs(xDataFFT)/totalNumberOfSamples, "lineWidth", widthOfTheLine);
set(get(gca, 'XLabel'), 'String', 'Frequency in Hertz  (Hz)');
set(get(gca, 'Title'), 'String', 'Un-Sampled Signal');
grid on;
axis([0 messageSignalFrequency+messageSignalFrequency/3 0 inf]);

We use the code with slight modification to plot the Perfectly Sampled, Under-Sampled and Over-Sampled signals.

% Plotting Under Sampled Signal
underSamplingFrequency = 1.2*messageSignalFrequency; % Deciding the Frequency for demonstraring undersampling
under_timePerSample = 1/underSamplingFrequency; % Time needed for a single sample
under_timeAxis = 0:under_timePerSample:stopTime-under_timePerSample; % Generating the time axis
under_totalNumberOfSamples = size(under_timeAxis,2); % Calculating the number of samples
under_samplingFrequencyInterval = underSamplingFrequency/under_totalNumberOfSamples; % Calculating the frequency interval to generate the frequency axis;
under_frequencyAxis = -underSamplingFrequency/2:under_samplingFrequencyInterval:underSamplingFrequency/2-under_samplingFrequencyInterval; % Generating the Frequency Axis
 
% In time Domain
subplot(423);
under_xData = sin(2*pi*messageSignalFrequency*under_timeAxis + phi);
hold on;
plot(1000*under_timeAxis, under_xData, "lineWidth", widthOfTheLine);
stem(1000*under_timeAxis, under_xData);
set(get(gca, 'XLabel'), 'String', 'Time in milliSeconds  (ms)');
set(get(gca, 'YLabel'), 'String', 'Amplitude');
set(get(gca, 'Title'), 'String', 'Under-Sampled Signal');
hold off;
grid on;
axis([0 1000*numberOfWaves/messageSignalFrequency -1 1]);
 
% In Frequency Domain
subplot(424);
under_xDataFFT = fftshift(fft(under_xData));
semilogx(under_frequencyAxis, abs(under_xDataFFT)/under_totalNumberOfSamples, "lineWidth", widthOfTheLine);
set(get(gca, 'XLabel'), 'String', 'Frequency in Hertz  (Hz)');
set(get(gca, 'Title'), 'String', 'Under-Sampled Signal');
grid on;
axis([0 messageSignalFrequency+messageSignalFrequency/2 0 inf]);

% Plotting Perfect Sampled Signal
 
perfectSamplingFrequency = 2*messageSignalFrequency; % Deciding the Frequency for demonstraring perfectsampling
perfect_timePerSample = 1/perfectSamplingFrequency; % Time needed for a single sample
perfect_timeAxis = 0:perfect_timePerSample:stopTime; % Generating the time axis %removed "-perfect_timePerSample"
perfect_totalNumberOfSamples = size(perfect_timeAxis,2); % Calculating the number of samples
perfect_samplingFrequencyInterval = perfectSamplingFrequency/perfect_totalNumberOfSamples; % Calculating the frequency interval to generate the frequency axis;
perfect_frequencyAxis = -perfectSamplingFrequency/2:perfect_samplingFrequencyInterval:perfectSamplingFrequency/2-perfect_samplingFrequencyInterval; % Generating the Frequency Axis
 
% In time Domain
subplot(425);
perfect_xData = sin(2*pi*messageSignalFrequency*perfect_timeAxis + phi);
hold on;
plot(1000*perfect_timeAxis, perfect_xData, "lineWidth", widthOfTheLine);
stem(1000*perfect_timeAxis, perfect_xData);
set(get(gca, 'XLabel'), 'String', 'Time in milliSeconds  (ms)');
set(get(gca, 'YLabel'), 'String', 'Amplitude');
set(get(gca, 'Title'), 'String', 'Perfectly-Sampled Signal');
hold off;
grid on;
axis([0 1000*numberOfWaves/messageSignalFrequency -1 1]);
 
% In Frequency Domain
subplot(426);
perfect_xDataFFT = fftshift(fft(perfect_xData));
semilogx(perfect_frequencyAxis, abs(perfect_xDataFFT)/perfect_totalNumberOfSamples, "lineWidth", widthOfTheLine);
set(get(gca, 'XLabel'), 'String', 'Frequency in Hertz  (Hz)');
set(get(gca, 'Title'), 'String', 'Perfectly-Sampled Signal');
grid on;
axis([0 messageSignalFrequency+messageSignalFrequency/2 0 inf]);
 
 
% Plotting Over Sampled Signal
 
overSamplingFrequency = 8*messageSignalFrequency; % Deciding the Frequency for demonstraring oversampling
over_timePerSample = 1/overSamplingFrequency; % Time needed for a single sample
over_timeAxis = 0:over_timePerSample:stopTime-over_timePerSample; % Generating the time axis
over_totalNumberOfSamples = size(over_timeAxis,2); % Calculating the number of samples
over_samplingFrequencyInterval = overSamplingFrequency/over_totalNumberOfSamples; % Calculating the frequency interval to generate the frequency axis;
over_frequencyAxis = -overSamplingFrequency/2:over_samplingFrequencyInterval:overSamplingFrequency/2-over_samplingFrequencyInterval; % Generating the Frequency Axis
 
% In time Domain
subplot(427);
over_xData = sin(2*pi*messageSignalFrequency*over_timeAxis + phi);
hold on;
plot(1000*over_timeAxis, over_xData, "lineWidth", widthOfTheLine);
stem(1000*over_timeAxis, over_xData);
set(get(gca, 'XLabel'), 'String', 'Time in milliSeconds  (ms)');
set(get(gca, 'YLabel'), 'String', 'Amplitude');
set(get(gca, 'Title'), 'String', 'Over-Sampled Signal');
hold off;
grid on;
axis([0 1000*numberOfWaves/messageSignalFrequency -1 1]);
 
% In Frequency Domain
subplot(428);
over_xDataFFT = fftshift(fft(over_xData));
semilogx(over_frequencyAxis, abs(over_xDataFFT)/over_totalNumberOfSamples, "lineWidth", widthOfTheLine);
set(get(gca, 'XLabel'), 'String', 'Frequency in Hertz  (Hz)');
set(get(gca, 'Title'), 'String', 'Over-Sampled Signal');
grid on;
axis([0 messageSignalFrequency+messageSignalFrequency/2 0 inf]);

The Output of the code:

Conclusion

We can see from the plots that the frequency of the Under-Sampled signal is not exactly same as that of the actual analog signal. When the frequency of the signal to be sampled was given as 200Hz, the frequency of the Under-Sampled signal was found to be 40Hz. This condition is also known as aliasing.
But the signal frequency of the Perfectly Sampled and the Over-Sampled signal is exactly same as that of the analog signal.

Tag Cloud

8051 Android android screen mirroring arduino Aria Aria2 assembly at89c51 blynk c cloud download client embedded c esp esp32 esp8266 firewall free domain name free website godaddy iot matplotlib namecheap networking nodemcu numpy pi hole platformio platformio with vscode programming pyaudio Python python 3 Raspberry Pi scrcpy seven segment display spectrum analyser toggle every second Torrent transmission vscode web hosting website without coding Web UI windows